Digd0g's Blog

达芬奇密码

发表于 更新于 分类于 ，
本文字数： 2.3k 阅读时长 ≈ 8 分钟
       
-------------已经到底啦！-------------
 

斐波那契数列

斐波那契数列

在解决这道题目之前我们首先先了解一下什么是斐波那契数列：
斐波那契数列的由来源于一位意大利青年，名叫斐波那契。在他的一部著作中提出了一个有趣的问题：假设一对刚出生的小兔一个月后就能长成大兔，再过一个月就能生下一对小兔，并且此后每个月都生一对小兔，一年内没有发生死亡，问：一对刚出生的兔子，一年内繁殖成多少对兔子?
为了更清晰一点，我们作出下面的示意图。

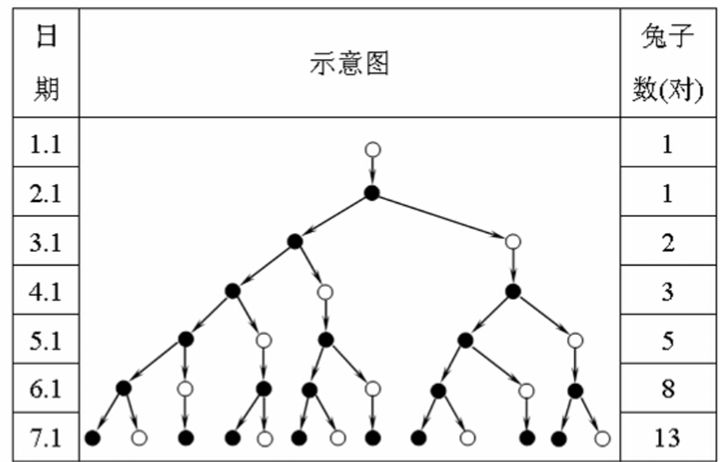
v2-2c689f0a974765945c0c36bd9571dab6_720w.jpg

在图中，我们的黑点表示的是成熟兔子，白点表示的是小兔子。我们够仔细的话能够发现，右边这一列数字是有规律的。第一个数和第二个数为1，之后的每一个数为之前两个数之和。比如，六月份的兔子数量为四月份和五月份兔子数量之和，即8=5+3。
此外，我们再仔细看一下，六月份的兔子中有五对黑（成熟）兔子和三对白兔子, 8=5+3。同样是8=5+3，但是该等式和上式中的5与3表示了不同的意义，那么他们之间是否存在本质的联系呢。实际上5对黑兔子就是上个月的5对兔子变来的，只不过其中的白兔子都变为了黑兔子，即5=5； 三只白兔子从哪来的，它们是四月份的三对兔子生的，不管黑白，到了五月份都是黑兔子，六月份的时候也就只有它们能生小兔子，而且必须生一对小兔子，所以3=3。

由此，我们甚至可以预测到未来的兔子数量

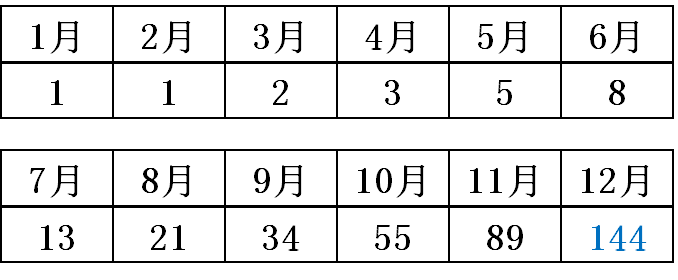
v2-daacceedc4abfe31b1bb29a7d3ba0913_720w.png

斐波那契数列的特性

斐波那契数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233……
观察一下上面的数列，你发现有什么特征吗？

  1. 第一项和第二项是1，之后的每一项为之前两项的和。

$a_1=a_2=1$

即：$a_n=a_(n-1)+a_(n-2)$

  1. 对每一项做平方

前几项平方求和求和：

$1^2+1^2$=2

$1^2+1^2+2^2$=6

$1^2+1^2+2^2+3^2$=15

$1^2+1^2+2^2+3^2+5^2$=40

$1^2+1^2+2^2+3^2+5^2+8^2$=104

………………….

我们观察一下等式右边

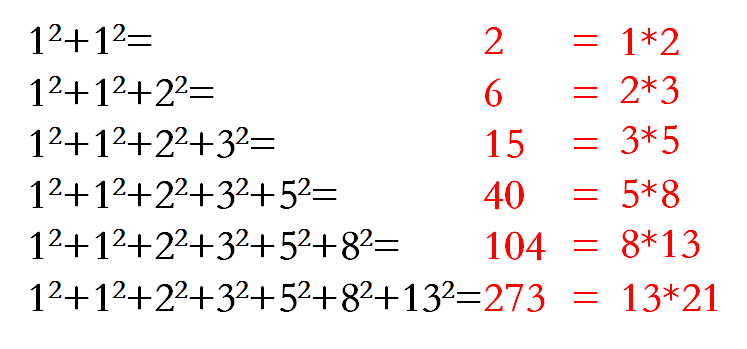
v2-4a25cbfaaf963251ff79a6a1be7d4a7e_720w.png
该等式右边中所有的数字均为斐波那契数，神奇吧。而且这不是一个巧合，这个性质不限于上式中的几个，事实上，我们可以写出前n项的平方和，依旧有这样的性质。为什么斐波那契数的前N项平方和可以写成两个斐波那契数之积呢？
既然这个性质不是巧合，那么其中必定有着更深层的数学本质。解决这个问题，我们从从上述的等式中貌似很难得到结论。我们转换一下思路，平方有何几何意义，显然平方指的是一个正方形的面积，那好，我们依照这个思路，作一个几何图形试试。

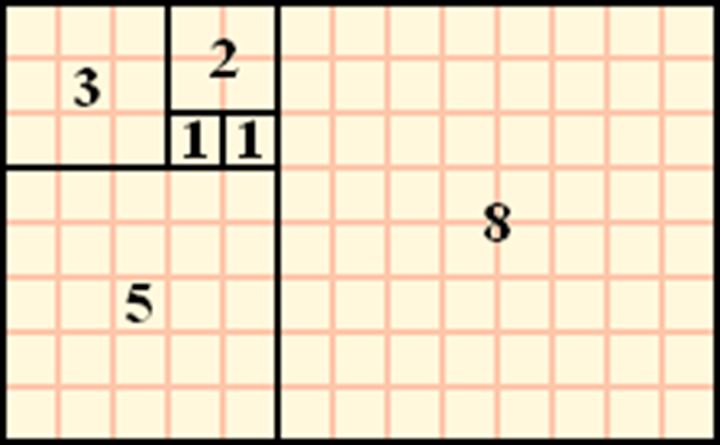
v2-36ea561a5aefcb023ddf5aa89098c352_720w.jpg

这下就很容易明白了，比如式中的第一个等式1^2+1^2=1*2。左边表示两个正方形的面积，右边表示一个长方形的面积，很显然它们表示的是同一区块的面积。再比如最后一个等式，左边表示上图中六个正方形的面积之和，右边表示图中的大长方形的面积，左右两边也是同一个区块。现在似乎明白了等式为什么成立了
我们只要知道当一个斐波那契数为其前n项平方之和，我们就可以构造上面的几何图形，而且这样构造的图形中的长方形(粗黑线为边界)的边长只能为斐波那契数。

  1. 左边为相邻两个斐波那契数的平方和，我们发现计算的结果全为斐波那契数

v2-2e93fa053d9596118d74736609a96082_720w.jpg

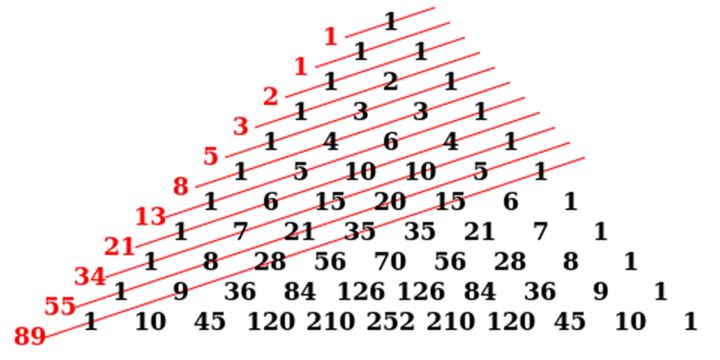
  1. 斐波那契数列与杨辉三角的关系

将杨辉三角中的斜向的一列数求和，得到一组新的数，而这一组新的数正好是斐波那契数列

v2-f367c8eaa7c2b324716f88eb46b30d1c_720w.jpg

  1. 斐波那契数列的整除性与素数生成性

每3个数有且只有一个被2整除，
每4个数有且只有一个被3整除,
每5个数有且只有一个被5整除，
每6个数有且只有一个被8整除,
每7个数有且只有一个被13整除，
每8个数有且只有一个被21整除,
每9个数有且只有一个被34整除，

…. …
… ….
生活中斐波那契数列也是很神秘的存在
大到宇宙银河
v2-5951c3331f817b27427d7b68f12207f7_720w.jpg
小到我们的手指
v2-bd85d2b44c3c059b1b53cd713f4888bb_720w.jpg
甚至是鹦鹉螺中都存在斐波那契数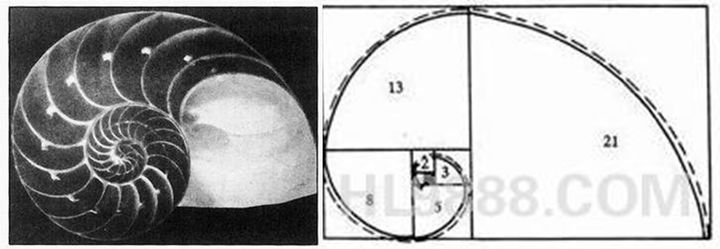
v2-b1fc486283bf20f4cb978001334ec9b2_720w.jpg

总地来说，斐波那契数列代表了神一样的递归思想。并在数论和计算机科学领域中长盛不衰。

参考

[1] O’Connor, John J.; Robertson, Edmund F., Leonardo Pisano Fibonacci//MacTutor History of Mathematics archive

[2] Dr R Knott. “Who was Fibonacci?”. Maths.surrey.ac.uk. Retrieved 2010-08-02.

[3] Weisstein, Eric W., “Binet’s Fibonacci Number Formula”, MathWorld.

[4] Douady, S; Couder, Y (1996), “Phyllotaxis as a Dynamical Self Organizing Process” (PDF), Journal of Theoretical Biology 178 (178): 255–74, doi:10.1006/jtbi.1996.0026

[5] Jones, Judy; Wilson, William (2006), “Science”, An Incomplete Education, Ballantine Books, p. 544, ISBN 978-0-7394-7582-9

[6] Brousseau, A (1969), “Fibonacci Statistics in Conifers”, Fibonacci Quarterly (7): 525–32

[7] Prusinkiewicz, Przemyslaw; Lindenmayer, Aristid (1990), The Algorithmic Beauty of Plants, Springer-Verlag, pp. 101–7, ISBN 978-0-387-97297-8

[8] Vogel, H (1979), “A better way to construct the sunflower head”, Mathematical Biosciences 44 (44): 179–89, doi:10.1016/0025-5564(79)90080-4

解题思路

现在回到题目

1
2
3
4
5
6
7
8
达芬奇隐藏在蒙娜丽莎中的数字列:

1 233 3 2584 1346269 144 5 196418 21 1597 610 377 10946 89 514229 987 8 55 6765 2178309 121393 317811 46368 4181 1 832040 2 28657 75025 34 13 17711


记录在达芬奇窗台口的神秘数字串:

36968853882116725547342176952286

这道题题目是达芬奇密码，我一开始猜想可能会和原著有关，于是去翻阅里面存在的各种密码

微信图片_20210905160715.jpg
不耐心，没找到。
但是
电影简介中会提到——斐波那契数列。贯穿整部电影的重要线索。
而隐藏在蒙娜丽莎中的数字列则是斐波那契数列

1
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 832040 1346269 2178309

对比蒙娜丽莎中的数字列，发现数值一样，但是进行了位移。
之后对比，观察题目中给到的两个数列的长度都是32，并且题目提示flag也是32位，可以推测，神秘数列是通过flag位移后得出的，而位移的规则是斐波那契数列的位移。

1
2
3
4
5
6
7
8
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 832040 1346269 2178309

1 233 3 2584 1346269 144 5 196418 21 1597 610 377 10946 89 514229 987 8 55 6765 2178309 121393 317811 46368 4181 1 832040 2 28657 75025 34 13 17711



3 6 9 6 8 8 5 3 8 8 2 1 1 6 7 2 5 5 4 7 3 4 2 1 7 6 9 5 2 2 8 6

对比两列数列：

第0位1还是1，没有位移。

第一位233是斐波那契数列中的第十二位（从第0位开始算），因此下面神秘数字串的第一位的6是原本flag的第十二位。（因为神秘数列是通过flag位移后得出的，而位移的规则是斐波那契数列的位移。我们通过斐波那契数列位移反推flag）

第二位3是斐波那契数列的第三位，因此下面神秘数字串的第二位的9是原本flag的第三位。

以此类推……

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
fb = '1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 832040 1346269 2178309'

t = '1 233 3 2584 1346269 144 5 196418 21 1597 610 377 10946 89 514229 987 8 55 6765 2178309 121393 317811 46368 4181 1 832040 2 28657 75025 34 13 17711 '

m = '36968853882116725547342176952286'
s = 'a' * 32
s = list(s)
fb = fb.split(' ')
t = t.split(' ')


for i in range(32):
    s[fb.index(t[i])] = m[i]
for i in range(32):
    print(s[i], end='')

这里补充一下python语法：
Python 列表 index() 方法
==index() 方法返回指定值首次出现的位置==

1
2
3
4
5
6
7
8
fruits = ['apple', 'banana', 'cherry']

x = fruits.index("cherry")

print(x)


返回为2

最后结果中带有一个a
微信图片_20210905163820.png

题目说的是32位十进制，可能是哪里出错了…

注意数字列中的第2个1在第24位，由于string.index()函数在查询下标的时候，会从右往左查询，故而第24位的1所对应的数字7，覆盖了第0个位置的1所对应的数字3。所以第1个位置没有数字，还是a