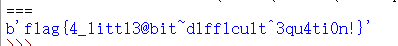-------------已经到底啦!-------------
RSA解密的入门题型
在此复盘前几日做的几道Crypto
where_is_my_flag
Download txt
1 | p = 0xbdb8699374e4def5d3f3463e772ee20c08e1315c58bc3a762bd7df0eaa2df1411f60b76af536d98dea06f9baf1ba8e4e0e6e9e82f77128301b9402c1c3f8295f11e4334579f5c4c1349a7e1f979600ea203c1ecce035af549d29a42f3088504c09b3074e8680c2ef7b1a1076ac5f247faf539e8999bd21b89d5ab0010dd582db |
编写一段python脚本跑一下
1 | import gmpy2 |

RSA-Equation
1 | p+q= 0x15554bf3279b5a5ff3a6f51348840a5c77f85d649ef89fe6f6aecca3b7a4f8954d94c041b9bf9c53605e69bf381df6b1e264dbe7cf3760d816bca53bc783efd62 |
1 | import gmpy2 |

RSA-Equation2
1 | n=16917955357177705838022522227269189799965442955600174230088241413537748036079610427667748524760416412487661588166675433898394627618977795412467578931925290358440662780942041112815203687805808800979128075090221137838151372846654787093946656482304031633775358207228010135390832522575861986102844835573116079075374771222923318301544600822685589433165393483870570768619713138725020836976344994143665005213595439734053715247430701190483139697651308683944225607919788529538100719847326451607419315958484481451634531624954226369336218518430937719669057217473641902380243356961565889376657557909528540953750939711249576195159 |
1 | import gmpy2 |